This is a continuation of our goals subtracted (g-) research, focused on evaluating defensive ability on set pieces. The first article focused on open play.

Introduction

This past summer we introduced a framework for evaluating the individual contributions of defenders, goals subtracted (g-). We concluded that–while it was a tricky problem, and not one that was obviously made easier even with tracking data–the framework had potential to help control for otherwise unmitigated interrupting g+ value. We observed players on bad defensive teams getting a lot of interrupting value largely because the ball is coming at them all the time, and g- hinted that it might be able to control for this. That article was about measuring open-play defending, and this article is about measuring set-piece defending. If you are unfamiliar with goals added (g+), I would start here with our primer.

I’ll steal the original introduction from myself: At the team level, evaluating defensive efficacy is actually not that hard. Expected goals allowed (xGA) or g+ allowed do a pretty good job of ranking teams’ defensive prowess in a meaningful way that predicts their future defensive performance. But how do you take all the goals, xG, or g+ allowed and allocate to individual players? It’s clear that Interrupting goals added–the value gained by making defensive actions–falls well short here. Tiotal Football had this to say when g+ came out in 2020:

“When a player interrupts or stops a +0.030 scenario by tackling the ball away to generate a +0.005 net goal difference scenario for their own team, the model awards +0.035 [Interrupting g+] to the defender (the change in the two game states). But what about all the times the player was not in position to intercept the pass or make the tackle or block the shot? And what about the fact that the defender is part of a defensive unit that allowed its opponents to move the ball [into the] +0.030 net goal scenario in the first place? It is a problem.”

In summary, the basic premise is this. Start with goals added (g+), and then invert it, debiting defenders who allowed the opponent to generate g+. More specifically, in various gamestates, across specific zones of the pitch, who was responsible for allowing g+ to pass through? Let’s tackle the complexities of measuring set-piece defending now.

Methodology

First of all, what is a set piece “circumstance”, or phase of play? The answer is less obvious once you start thinking about it. Clearly a shot directly off a corner-kick cross is an action stemming from a set piece, and the g+ earned there by the attacking team should be categorized as set piece value allowed. But what happens if the corner is cleared out toward the half line, back to the corner kicking team? Is the next action part of a set piece or open play? What about the action after that? I opted to tweak our definition of open play vs. set pieces slightly as I worked more on this problem, and here’s what qualified as a set piece for this research.

An action is considered part of a set piece phase of play if the current possession recently saw a set piece action, where recently is defined is the following ways:

The possession is within 10 possessing actions from a corner kick
The possession is within three (changed slightly from five in our previous iteration) possessing actions from a goal kick or throw in
The possession is within 10 possessing actions from any other sort of free kick

This definition leaves us with about two-thirds of all relevant, non-interrupting actions being categorized as “open play” and the other third being categorized as coming from set pieces.

With that definition above of set piece actions, we turned to the next step, where we determined who is responsible for allowing the other team to accumulate offensive g+ value during these set piece phases of play. We followed our original logic of determining zonal responsibility by position–essentially deriving which positions were responsible for defending which actions on average. The trick here is to generate play types, or circumstances, that are granular enough to reasonably identify where positions “should be” defending, but general enough so as to have a decent sample size and not blow up my computer.

Here's what we did differently from before to find those responsible for allowing g+ value in set piece situations. It would definitely be worth reviewing that original methodology if you enjoy the details.

Used only interrupting actions to determine positional responsibility by circumstance. In open play, players’ offensive actions may give us some better insight into where their position should be defending, but for set pieces–where each player typically has a chance to reset their position–we focus only on interrupting actions.
Included keepers in set-piece zonal responsibility. This led to silly results when I tested the inclusion of keepers in our open play framework, but much more reasonable results for set pieces. A typical keeper takes on about 1.5x the amount of g- (i.e., g+ allowed) as a center back, who in turn take on about 1.2x the amount g- as a wingback, all of whom take on more g- than non-defender positions. This seemed reasonable.
Further segmentation of “circumstances”:

35 action zones. Where was the offensive action (i.e., the g+ generated against) completed? This is clearly important, as we wouldn’t expect centerbacks to be defending short goal-kick passes, for example. We took the 30 zones from the first iteration (which can be seen on our g+ tab here, and shown below) and split the first five zones right in front of the defense’s endline into 10 zones. This helps better separate out the keeper from defenders, among other allocation benefits.
Set piece origin. Did the original set piece action come from the attacking wing (e.g., corner), top of the box (e.g., set piece shooting zone), or a more defensive location (e.g., goal kick). Again, center backs won’t be defending short balls off goal kicks. The type of set piece (kicked vs. thrown) and where it was taken from are crucially important for determining who is responsible. We tried further breaking up kicks by type (e.g., free kick from the wing vs. corner kick), but it ended up making working better to use the action zones and set piece origin zones noted above. You can only chop historical possession up so finely before you end up with no observations in some “circumstances.”
Kicked vs. thrown. Hopefully self explanatory.

Figure: Set piece responsibility zones

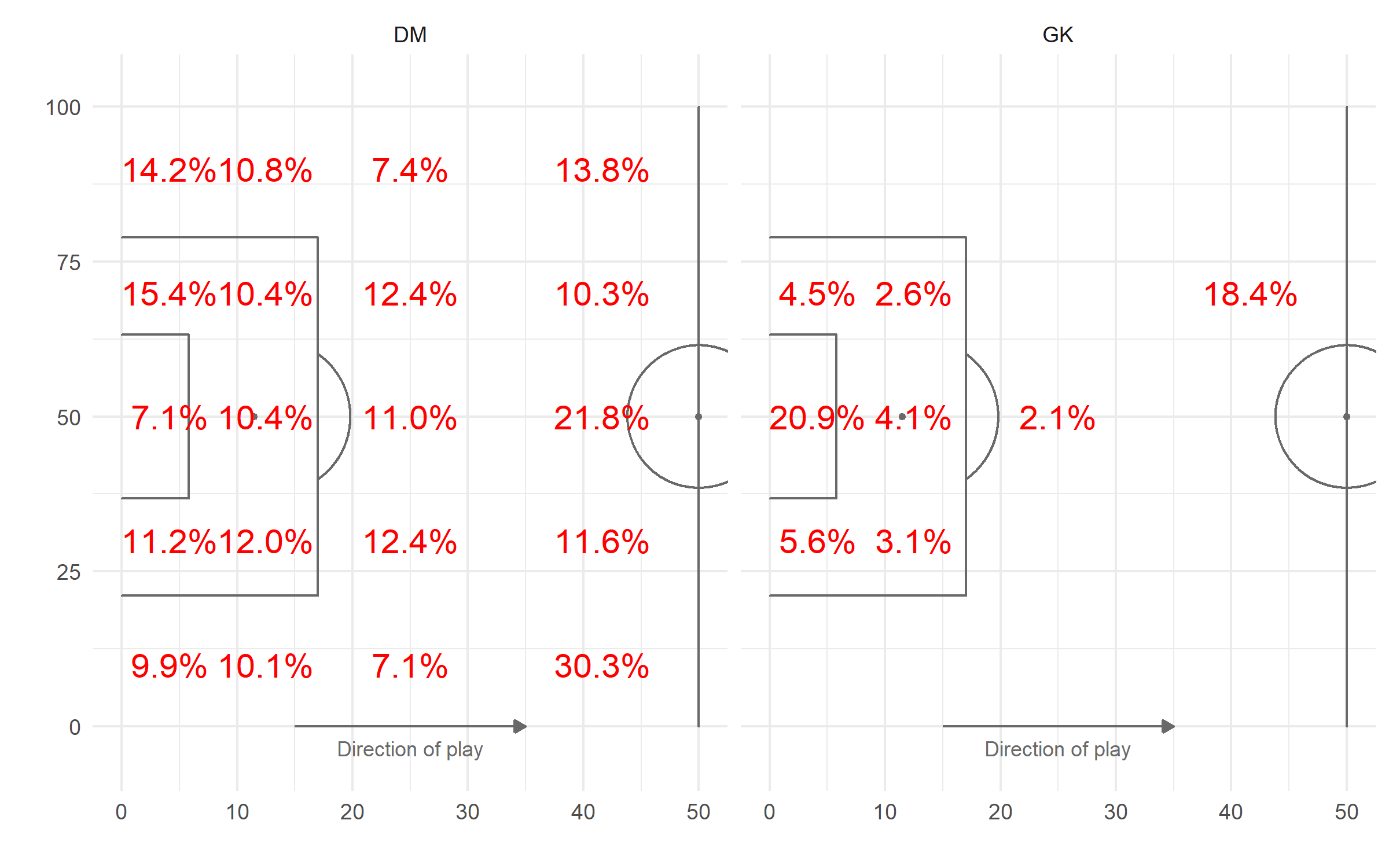
Let’s take a look at some of the intermediary outputs by position to get comfortable. Here we look at the typical zonal coverage by position, specifically comparing defensive midfielders (DMs) to goalkeepers (GKs). We have further filtered to dangerous free kicks originating from the wing, close to the endline (i.e., from zones 5, 10, 1, or 6). This includes corner kicks. The plot below shows where the defenders of each position tend to make defensive actions on such free kicks.

Using (set-piece) zone 3 as an example, in set-piece situations like these, DMs complete 28.7% of their defensive actions in this zone in front of the goal, while GKs complete 90.2% of their actions in zone 3. Because, of course GKs are intercepting crosses and saving shots right in front of the goal. Certainly DMs are clearing balls from this zone as well, but their zonal coverage extends to many other zones in the defensive half. Later the math described in the original article will make GKs approximately 90.2/28.7 ~ 3 times as responsible as DMs for zone 3 on these types of set pieces. (The math is actually done at a much more granular level than this aggregated view, so it’s not exactly 3.14 as calculator wizards will later point out).

Figure: Zonal coverage by position, on dangerous free kicks from the wings and corners

Note, the plot above did not show each position’s zonal responsibility relative to other positions, but rather their zonal coverage within their position, summing to 100% for each position. When we consider all the positions at once, we normalize each coverage zone such that the sum of all positions’ responsibilities in that zone is 100%. When a ball sails into zone 3, right in front of the goal, which positions are most responsible? Let’s take a look at position responsibility for GKs and DMs on these dangerous free kicks from the wing. Focusing on zone 3 again, we see that GKs are responsible for 20.9% of the g+ value allowed in here, while DMs are responsible for just 7.1%. This makes sense! At east, directionally. We can quibble about magnitudes later.

As derived above, GKs are about 20.9/7.1 ~ 3 times as responsible as DMs in this zone. If we were to add up the zonal responsibility in zone 3 of all positions on the field during a particular game-segment, we would get 100% for each set piece origin (e.g., free kicks from wing).

Figure: Zonal responsibility by position, on dangerous free kicks from the wings and corners

Finally, when looking at raw g- and overall Defense scores by position, we notice that the more defensive positions are taking the biggest hit. Defense scores are simply a balance of open play g-, set piece g-, and interrupting g+, and negative is bad. Some of this bias against the defensive positions is likely because it’s their job to play defense, so of course they allow the most value through their zones.

Additionally we see midfielders getting comparable amounts of interrupting g+ to defensive players, but taking on a noticeably lower burden of g+ allowed (i.e., g-). Some of this may be due to a bias discussed in the Future Considerations section, and some might be that midfielders are able to make valuable interrupting actions up the pitch, without being held responsible for large amounts of g+ allowed in their own box. Regardless of why, we’ll continue waving our magic wands and normalizing each position, such that the average player within each position allows 0.00 g- “above average”.

Table: Raw g- and interrupting g+

Pos	Min	Int g+/96	Open g-/96	Set g-/96	Def/96
RCM	116,822	0.072	-0.085	-0.030	-0.042
DM	194,534	0.078	-0.089	-0.031	-0.042
LCM	104,425	0.065	-0.085	-0.030	-0.050
RM	85,055	0.045	-0.075	-0.028	-0.058
AM	125,396	0.047	-0.079	-0.027	-0.058
LM	85,261	0.047	-0.077	-0.029	-0.059
LB	185,140	0.065	-0.086	-0.039	-0.060
RB	187,149	0.065	-0.089	-0.039	-0.062
F	327,480	0.034	-0.077	-0.028	-0.071
GK	185,637	-0.003	0.000	-0.070	-0.073
CB	60,567	0.075	-0.120	-0.040	-0.085
RCB	191,799	0.081	-0.132	-0.044	-0.096
LCB	187,868	0.076	-0.131	-0.045	-0.100

2022 Results

These results have been normalized by position, as discussed above, allowing center backs like Jack Elliot to shine. The g- values shown are in units of “goals allowed above average per 96 minutes,” and perhaps somewhat intuitively positive values are good. Much like for goalkeeper shotstopping and overall g+ scores, we want to stick with the notion that positive values are good, as this is a value metric.

Top defenders

Player	Tm	Min	Pos	Open g-	Set g-	Int g+	Def g-
Jack Elliott	PHI	3167	LCB	0.039	0.005	0.087	0.132
Mamadou Fall	LAFC	1338	LCB	0.053	-0.003	0.018	0.068
Auston Trusty	COL	1589	LCB	0.032	-0.012	0.044	0.064
Franco Escobar	LAFC	1264	RB	0.015	0.009	0.038	0.062
Javain Brown	VAN	2030	RCB	0.029	-0.002	0.030	0.058
James Pantemis	MTL	1104	GK	0.000	0.038	0.017	0.055
Alejandro Pozuelo	MIA	1048	F	0.001	-0.007	0.060	0.054
Diego Palacios	LAFC	2669	LB	0.025	-0.004	0.033	0.053
Cristian Arango	LAFC	2562	F	0.024	0.004	0.025	0.052
Nouhou Tolo	SEA	2748	LCB	0.026	0.004	0.021	0.051

Worst defenders

Player	Tm	Min	Pos	Open g-	Set g-	Int g+	Def g-
Carlos Salcedo	TOR	1316	CB	-0.088	-0.007	-0.111	-0.205
Dario Zuparic	POR	2455	LCB	-0.050	-0.022	-0.073	-0.145
Tony Alfaro	DCU	1062	LCB	-0.074	-0.008	-0.050	-0.133
Brent Kallman	MIN	1524	LCB	-0.056	-0.017	-0.022	-0.095
Jonathan Bell	NER	1145	LCB	-0.034	-0.002	-0.054	-0.089
Jackson Hopkins	DCU	1009	LCM	-0.013	0.000	-0.067	-0.081
Steve Birnbaum	DCU	3162	CB	-0.048	-0.011	-0.017	-0.076
Zeca	HOU	1263	RB	-0.010	-0.020	-0.045	-0.075
Lukas MacNaughton	TOR	1975	RCB	-0.047	-0.001	-0.025	-0.073
José Van Rankin	POR	2087	RB	-0.018	-0.016	-0.035	-0.070

Stability

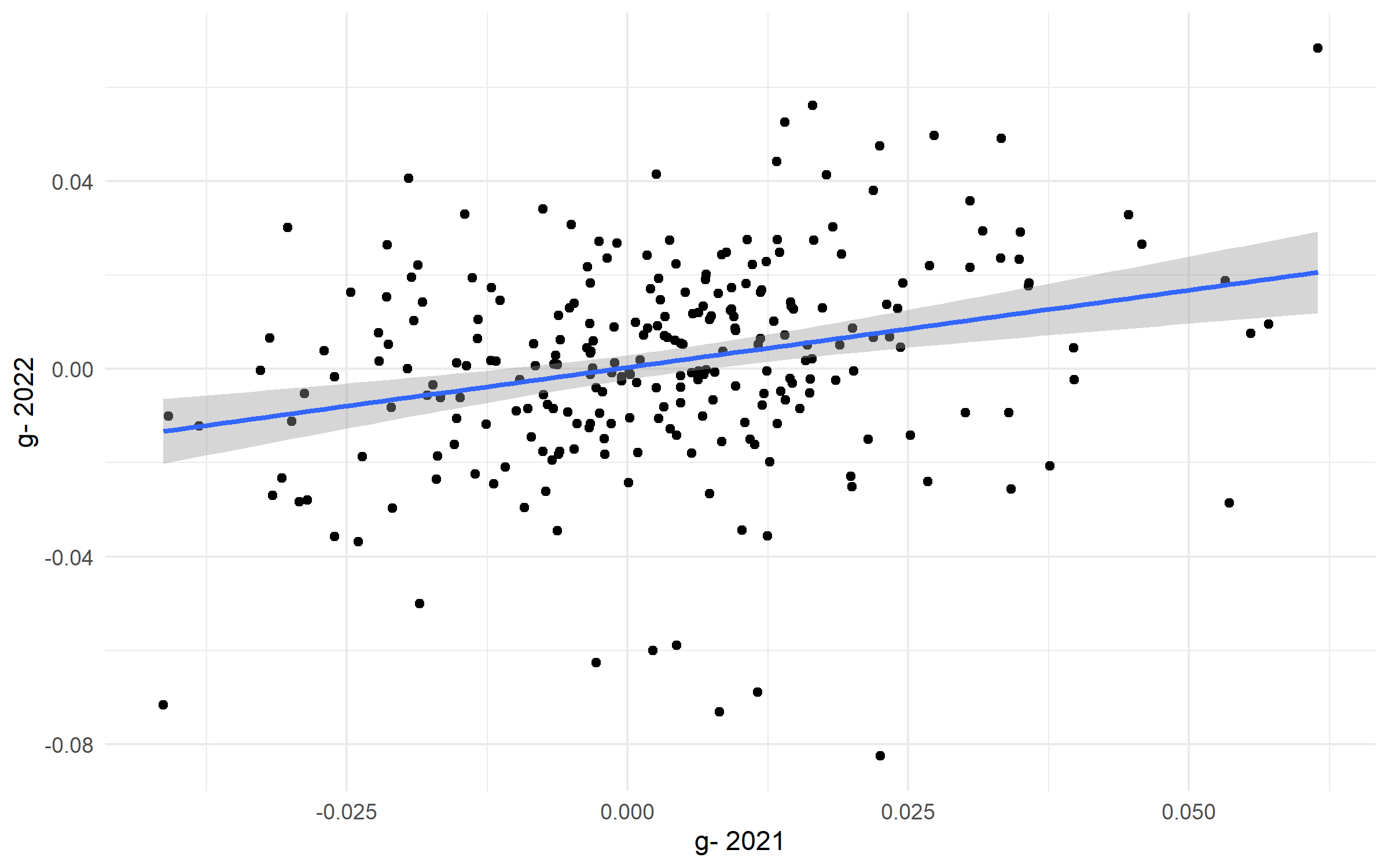
One way to measure the utility of a metric is to ask whether it predicts itself. I gathered 259 players that played at least 1,000 minutes in both 2021 and 2022 and plotted their seasons against each other. The slope of the line in the figure below is about 0.33, and one way to interpret that slope is to infer that players regress toward the mean in g- about 67% from season to season, but 33% of their performance is true signal. That’s not actually that bad.

Figure: Total g- by player, 2021 vs. 2022, greater than 1,000 minutes played in each season

However, there is (at least) one notable flaw with the above approach. Most of these players, 227 to be exact, played on the same team both years, and this correlation may be more due to team effects than player effects. Indeed, the slope for those 227 players who stuck with the same club was more than 0.40 (40% year-over-year stability), but the slope for the 32 players who changed teams was statistically insignificant and negative. Hmmmm. So I normalized each player’s g- value within his team and ran the regression again. This helps control for the team effect, and measures whether players perform similarly season over season relative to their teammates.

With the 1,000 minute cutoff in both seasons, the overall slope fell from above 0.30 to below 0.10, and was no longer statistically significant. With a 2,000 minute cutoff, the slope bounced back up to nearly 0.30 for players staying on the same team. In other words, relative to their teammates, bad defenders were more likely to be bad defenders again, and good defenders more likely to remain good defenders, but with a fair amount of regression to the mean.

It’s hardly conclusive, but I think we can say two things fairly confidently: (1) when it comes to defense, team defense is more than an aggregation of individual defenders, and (2) bigger sample sizes improve stability year over year. We can check out the stability of g- again when we build this out across more seasons and more leagues, to try to confirm that the 30% slope, or “stability score”, is actually true.

Future considerations

Defender bias

While reviewing the results in aggregate, we noticed a clear bias hurting players that make a lot of interrupting actions in front of the goal. This became most obvious when we added goalkeepers to the open-play position list as an experiment. They took 67% of the responsibility for the area just in front of their goal (open play zone 3, technically) and thus they took a huge g- burden, two-to-three times that of any other position in total. That just seemed wrong. To a lesser extent this happens to centerbacks, too, both in set pieces and open play. For set pieces, we created more granular zones in front of goal to help with this issue, and we may just need to go even more granular.

If you’re wondering how this bias happens, think about this hypothetical: a ball comes flying into the box, and it's toward your beast of a center back. They win the ball because they win these balls 75% of the time, and thus get many interrupting touches for doing their job. This also adds to their zonal responsibility burden. A second ball swings in toward your short defensive center mid, who is dropping in for a set piece or other dangerous attack. They watch the ball fly past, and only win these types of balls 25% of the time, because they are short and bad at The Defense. The overall positional responsibility ends up getting weighted toward center backs for essentially doing their job, while their mates basically suck and don’t get the interrupting touches which populate the numerator of zonal responsibility. There’s nothing to catch bad defenders not being there. The solution? We need DUELS (duels enthusiasts rejoice). Specifically, we need lost duels to help better understand who is responsible for a given plot of land. Duels weren’t readily available in our data during this research, but this is definitely a plug for duels if you were looking for a plug for duels.

Circumstance segmentation

Again, with the goal of determining who should be where and when, we could segment more. Further splitting by home and away, for example, would combine with gamestate (already in the framework) to possibly better explain how offensive or defensive certain positions tend to play, and where we should expect those players to be playing. But we have to be wary of over-segmenting the data, which creates small groupings from which to derive zonal responsibility, and also blows up my computer. Right now, the set piece coding pipeline, for a brief moment, generates 100 million combinations of things. I had to implement some slick tricks to get it to work with just 2 seasons already.

Set piece and open play definitions

Regarding how set pieces are defined distinct from open play, we did not test those thresholds for this analysis. In retrospect, specifically the 10-action threshold for when a free kick becomes open play seems long, and we could probably quibble over others, as well. Maybe there should even be a third “phase”, distinct from open play and set pieces, that refines these middle grounds. That gets into another piece of information that could help answer the question who should be where and when. We discussed further controlling for how far into the possession we are, like how many actions have been completed to get to this point, which would help define the phase of play, players' roles, and the resulting zonal responsibility weights between interrupting and offensive action locations by position.

I guess the only way to conclude this is to thank you for making it to the end!

American Soccer Analysis

Goals Subtracted (g-): Set piece edition