PScore, Tactics and game theory in MLS
/By Jared Young (@jaredeyoung)
Once we get an understanding of a team’s tactical preferences we can start to examine the best ways to respond to their approach. Using simple game theory we can start to look into the mind of a coach as he prepares his team. For example, the Seattle Sounders have consistently been a proactive team the last few seasons (and currently rank 2nd in the P Score Index in 2015). If you are a proactive team as well, and you’re about to visit the Sounders, do you go toe to toe with them and try to win the possession battle? Or do you play more reactively, sit back and play longer balls over the top of their aggressive defense?
In the June recap of the PScore (click here for May's recap), which scores a team’s proclivity to be possession oriented versus more direct in their approach, I’m going to analyze some tactical decisions and use game theory to determine the best mode of operation. I’ll even check to see if Nash Equilibriums exist (where both teams should definitely play a certain style regardless of the knowledge of what the opponent is doing). I do need to start by saying that sample sizes are still pretty small despite MLS having played 173 matches, so all conclusions must be taken with a grain of salt, or at worst not be considered conclusions. But at the very least I hope to lay the groundwork for future exploration in this area. It also serves as another check to see if the P Score is actually making logical sense.
First here is the current P Score table through the end of June.
| Team | Rank | Last | P Score |
|---|---|---|---|
| ORL | 1 | 1 | 7.7 |
| SEA | 2 | 3 | 6.2 |
| MON | 3 | 2 | 6.1 |
| NYRB | 4 | 4 | 5.9 |
| TOR | 5 | 9 | 5.9 |
| CLB | 6 | 5 | 5.8 |
| LA | 7 | 10 | 5.6 |
| DC | 8 | 7 | 5.6 |
| POR | 9 | 12 | 5.6 |
| PHI | 10 | 17 | 5.4 |
| HOU | 11 | 11 | 5.4 |
| NYCFC | 12 | 6 | 5.4 |
| CHI | 13 | 8 | 5.3 |
| NE | 14 | 13 | 5.2 |
| VAN | 15 | 14 | 4.9 |
| SKC | 16 | 16 | 4.7 |
| DAL | 17 | 20 | 4.4 |
| SJ | 18 | 15 | 4.4 |
| COL | 19 | 18 | 4.3 |
| RSL | 20 | 19 | 3.9 |
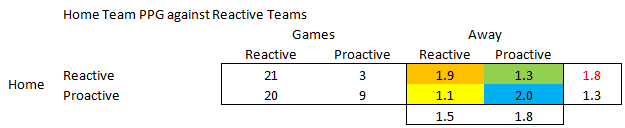
For the purposes of the game theory discussion I created a list of proactive teams and reactive teams. The top six teams, Orlando through Columbus, are the league’s proactive teams. And the bottom six teams are the most reactive, from Vancouver to Royal Salt Lake. The rest are in what I call no man’s land. The reason I call it that is because those teams are weaker than those at the PScore poles.
Data seems to support this in every post; it pays to commit to one style of play versus the other. Being somewhere in the middle is not optimal. If you take DC United out of that equation the PPG of that groups drops even more to 1.2. But the other point of this chart is to show that Proactive and Reactive teams are equally competent in this league, at least this year.
Let’s jump right in and start with an overview of this game theory idea. Here is a chart of all the games played in MLS in 2015 from the perspective of the home team. I have grouped games scored with P Score 1-5 as reactive and 6-10 as proactive. On the left hand side are the number of games played and in the colored boxes is the point per game for the home team given the team’s style of play. For example, if the home team plays proactively and the away team plays proactively then the home team on average gets 2.2 points per game, over 39 such games played.
Here we can see that home teams have a very slight advantage playing reactively (1.8 versus 1.7). Without thinking of their opponent a coach might be inclined to direct his team to sit back and then strike on the counter. Now here is the away team’s perspective.
It appears they should play reactively as well. But if the home team and the away team both play reactively the away team is only able to secure 0.8 points. So if the away team knows the home team is playing reactively then they should play proactively, because if they do, their points per game will increase to 1.2. But if the home knew that the away team were playing proactively then they too should play proactively because they could increase their points per game to their optimal state of 2.2. If the away team knew the home team was playing proactively then then would choose to play reactively, which is the worst outcome for the home team, who would then also choose to play reactively. So, it’s an endless cycle with no equilibrium where clearly knowledge of the opponent can inform a tactical decision. This makes logical sense in that if a team has knowledge of another team’s tactics, they should benefit from that knowledge.
With the P Score we can now look at the likelihood that teams will play a certain style and see if game planning for them reaches any points of equilibrium. We can start to use out segmentation of teams to get different views of the same data. I’ll start with a rather dull result but it gets the brain thinking along the lines of the game.
Teams that are traveling to a reactive team will 71% of the time pay reactively, but it doesn’t matter what they play without knowledge of the opponent. However, if the away team knows the home team will be reactive, which they are 65% of the time, then they can eek out another point if they play proactively.
For the home team the ingoing outcome is the same. However, if they consider the likelihood that the away team will play proactively to earn that extra point, then it’s in their best interest to play proactively. If the away team knows the home team will play proactively then they could get another point by playing reactively. Again we’re in the endless cycle. In this example the impacts are small and mostly like the product of noise given the sample sizes. But at least we’re getting this game down.
How about when a reactive team visits another team?
When welcoming a reactive team to their field it appears the team should strongly consider playing reactively. If they knew the reactive team were going to surprise them and play proactively then they should as well but here the sample is small, as this happens infrequently. It’s appears to be a really bad idea to play proactively against a reactive team when at home. It happens 47% of the time but it’s the worst outcome for a home team. This makes logical sense in that proactive teams can play into the hand of a reactive team. It appears the safest thing to do it play reactively and snuff out their counterattacks.
Reactive teams have a slight advantage to play reactively and there is just not enough evidence to suggest they should play proactively. They should just hope that the home team chooses to play proactively against them.
Let’s turn the attention to playing proactive teams.
Here we come the closest to finding a Nash Equilibrium. The visiting side should set out to be reactive, because they definitely want to avoid going toe to toe with a committed proactive team, where they would earn just 0.3 points per game. On the rare chance that a proactive team might play reactively at home it looks like the away team might want to switch to playing proactively but the sample sizes are very small. This is in fact what we see in most David verse Goliath matchups. If Crystal Palace were to visit Manchester City, we could be certain that Crystal Palace would cede a large amount of possession, try to keep large numbers behind the ball and hope to spring on the counter. It’s really their only chance of success. Here’s the other side of the equation.
And lastly let’s look at hosting a proactive team. Going into the game there appears to be no advantage but you can quickly see that the home team should mirror the style of the visitor.
The away team coach might see that there is a slight advantage to playing proactively on the road and there is slightly more upside in the best case (1.4) and no downside in the worst case (0.8) and he might come in with a proactive mindset. Thinking this the home team coach would then employ a reactive style.
We started with a look at all the games mashed together by home and away and we found that there was an infinite loop in terms of changing strategy based on what the other team was doing. But by looking at the tendency of teams to play a certain style of soccer we can see that the decisions on how to set the style of play become more clear. We can see that good proactive teams should almost always continue playing proactively. We can observe that the best way to approach a reactive team is to play reactively. Overall, the style of play matters far less for reactive teams where the difference in outcomes is much smaller. This sort of makes sense as a byproduct of the reactively style is to keep a closer match, since the play is more conservative defensively speaking.
There are a number of issues with this analysis that I should run through. I’ve mentioned and shown the sample size issue which will only be solved with time. The other is the influence of changes to strategy within the game. This analysis looks at a game in the rear view mirror and makes a binary decision about their style. It may have shifted in the middle of the game based on the score or other factors like red cards. I do believe game state has some influence on these findings but not enough to change the direction this line of thinking is headed. In addition, coaches may fake out the opponent early in the match to get a feel for their style and then switch tactics. This may cause their game to be scored in No Man’s Land when in reality specific tactics were changing throughout. It most definitely benefits a team to be flexible tactically.
There are also a lot of opportunities as well. Obviously more sample size will enable a deeper look at proactive versus reactive teams directly and gain more confidence in the insights. Rather than a binary split, I could also get more granular with the level of proactivity or reactivity. And of course you could start looking at specific teams to see what opponents they play what style against and how well they perform when certain styles are deployed against them.
My hope is that by reading this post you’ll be more critical of your favorite team’s tactical approach to the game. Perhaps when a proactive team comes to town you can watch for how high the defensive line is and how direct the team is playing. How successful are they playing with different approaches?